ТЕОРИЯ ПРОЧНОСТИ ТОНКИХ ВОЛОКОН

Прочность стекла

 

А.И.БОЛУТЕНКО

 

E-mail: bolutenko@mail.ru                 Физика стекла               Главная

 

 

АННОТАЦИЯ

 

     На примере стеклянных волокон рассмотрены существующие взгляды на прочность тонких волокон. На основе представлений о пониженной энергии поверхностного слоя конденсированных тел построена математическая модель прочности тонких волокон. Теоретическая кривая зависимости удельной прочности стеклянных волокон согласуется с литературными экспериментальными данными. Высокая прочность тонких волокон связана с повышенной прочностью поверхностного слоя.

 

 

     Рассмотрим феномен высокой прочности тонких волокон на примере стеклянного волокна. Большинство физико-химических свойств массивных стёкол и стеклянных волокон идентичны и определяются химическим составом. Значительно меньший вклад химического состава в прочность на растяжение, которая зависит от размеров образцов и увеличивается у тонких волокон. В то время, как прочность на растяжение массивного стекла составляет всего 80-150 МН/м², прочность волокна достигает до 4000 МН/м² [1], а прочность для кварцевых волокон 5000-6000 МН/м² [2].

     Первым сделал попытку объяснить резкое повышение прочности стеклянных волокон Гриффитс [3]. Он установил, что удельная прочность стеклянных волокон на разрыв возрастает по мере уменьшения диаметра, и объяснил этот факт ориентацией молекулярных групп в поверхностном слое волокна. В дальнейшем предпринимались новые попытки объяснения уникального свойства стеклянных волокон – повышенной механической прочности. В работах [4, 5] было выдвинуто предположение, что главную роль в повышенной прочности волокон играет масштабный фактор. Такие волокна имеют меньшую поверхность, это уменьшает вероятность наличия дефектов на поверхности и снижает их опасность. В работе [6] повышенная прочность стеклянных волокон объясняется ориентационным эффектом.

     Неудовлетворённость объяснениями прочности волокон ориентацией и масштабным фактором привела к поиску причин в технологических особенностях формования волокон. Предполагалось, что прочность стеклянных нитей обусловлена темпом охлаждения, не позволяющим получить микрогетерогенные структуры [7, 8]. По [9, 10] высокая прочность тонких волокон связана, прежде всего, с уменьшением величины и числа опасных дефектов, что зависит от метода и условий выработки волокон и их химического состава.

     Хотя не предложено никакого механизма упрочнения в процессе вытягивания, основным физическим фактором, приводящим к высокой прочности стеклянных волокон, в работах [11, 12] считается вязкая деформация в процессе вытягивания. Именно в результате вытягивания волокно приобретает прочность на растяжение во много раз большую, чем массивное стекло, что связывается с изменениями в поверхностном слое в результате миграции ионов [13].

     Ряд авторов считает, [8, 10, 14-16], что у тонких волокон благодаря высокой скорости охлаждения изменение структуры не успевает следовать за изменением температуры. В волокнах «замораживается» структура наиболее однородного высокотемпературного расплава, которая и определяет их высокую прочность.

     Следующим предположением, привлечённым к объяснению высокой прочности стеклянных волокон, было наличие тонкого упрочнённого поверхностного слоя толщиной порядка 5-10 нм. Этот слой образуется при формировании волокон из-за высокоэластичной деформации их поверхности [17]. Повышенная прочность поверхностного слоя снова объясняется молекулярной ориентацией [18] или просто отличием его структуры от структуры внутренних слоёв [19].

     Кроме отдельных причин, приводящих к высокой прочности стеклянных волокон, некоторые исследователи связывают эффект упрочнения с рядом одновременно действующих факторов. Это по [20] высокая прочность самой структуры реального стекла и технология получения волокон, обеспечивающая бездефектность поверхностного слоя. В работе [21] высокая прочность волокон объясняется масштабным фактором, фиксацией гомогенной структуры расплава, отсутствием остаточных напряжений и ориентацией микротрещин вдоль волокна. Также ряд факторов влияет на прочность волокон по [12]: высокая прочность структуры стекла, упрочнённый поверхностный слой и технология получения, исключающая опасные поверхностные дефекты.

     Как видно из обзора, существует достаточно много различных взглядов и гипотез объяснения высокой удельной прочности на растяжение тонких стеклянных волокон. Одновременно с развитием гипотез о прочности стеклянных волокон подвергалась сомнению правильность этих взглядов. В работах [8-10, 22] высказано мнение и экспериментально показано, что стекловолокно не имеет ориентированной структуры, и высокая прочность волокон не связана с молекулярной ориентацией. Возражения против гипотезы трещин, присущих структуре стекла, и недейственность на этом основании масштабного фактора, высказаны в работе [23]. Представления об отсутствии микрогетерогенностей в связи с технологическими особенностями выработки также не обоснованы, так как установлено, что массивное стекло и волокно имеют примерно одинаковые неоднородности [22]. Механизм упрочнения стеклянных волокон в связи с процессом вязкого течения как был не ясен ранее [11], так же трудно судить о нём и сейчас [12]. Представления о повышении прочности волокон в связи с вытяжкой не могут быть признаны правильными [24]. По работам [2, 9, 17] структура массивного стекла и волокна идентична, и объяснять прочность волокон замороженной высокотемпературной структурой не имеет смысла.

     Уже на протяжении длительного времени решается вопрос повышенной прочности тонких стеклянных волокон. По мере развития представления о прочности волокон носили противоречивый характер. До сих пор не ясна сущность явления повышенной удельной прочности тонких стеклянных волокон (и тонких волокон и плёнок вообще).

     Прочность стеклянных волокон одинакового диаметра имеет значительный разброс [4]. На практическую прочность сильное влияние оказывают микронеоднородности структуры, поверхностные трещины и другие дефекты. На степень опасности дефектов указывают уровни прочности, которые наблюдаются на стеклянных волокнах [25].

     Собственная прочность стеклянных волокон маскируется целым рядом дефектов, присущих материалу или возникающим во время изготовления волокна. Поэтому в вопросе о прочности волокон важно знать не фактическую прочность, которая определяется комплексом факторов, а прочность, связанную с идеальной структурой стекла. Перейдём от реальных стеклянных волокон к рассмотрению гипотетического бездефектного волокна, структура которого не имеет микронеоднородностей, ликвационного расслоения, микроскопических включений и волокна не имеют микротрещин.

     Что бы ни приводило к повышенной удельной прочности тонких стеклянных волокон, но экспериментально установлено для ряда стёкол увеличение удельной прочности на растяжение с уменьшением диаметра волокна. В поверхностном слое стеклянного образца преимущественно сосредоточены все дефекты. Заменим массивный стеклянный образец эквивалентным ему по площади большим количеством тонких нитей. Так как наиболее опасны поверхностные дефекты, то суммарная прочность таких нитей должна быть меньше прочности массивного образца. Однако, этого не происходит. Несомненно, суммарное количество дефектов поверхности в случае тонких нитей значительно больше, но прочность выше. Значит, наряду со снижением прочности от дефектов действует ещё какой-то фактор, который значительно повышает прочность волокон.

     Этим фактором может быть поверхностная энергия стекла. В теории прочности стеклянных волокон Гриффитс [3] использовал представления о поверхностной энергии, но лишь для определения критических напряжений роста трещин. В работе [26] отрицается возможность применения поверхностной энергии для описания механических свойств твёрдых тел.

     Обычно считается, что в связи с различной плотностью на границе раздела фаз частицы твёрдого тела образуют поверхностный слой с повышенным запасом энергии – поверхностный слой твёрдого тела [27-29]. Этот слой является пограничным между средой и внутренними частями тела.

     В работе [30] показано, что представления о повышенной энергии поверхностного слоя ошибочны. Поверхностный слой любого конденсированного тела имеет более низкую энергию, чем его объём. Для разрыва поверхностного слоя стеклянного волокна требуется повышенная энергия, то есть удельная прочность поверхностного слоя выше прочности внутренней части.

     Поверхность при разрушении твёрдых тел играет большую роль, но гипотезы прочности волокон не учитывают влияния поверхности. Хотя прочность поверхностного слоя выше, поверхность при разрушении массивных твёрдых тел не может дать большого вклада в повышение прочности. Но коренным образом положение меняется в микротелах: вклад повышенной прочности поверхностного слоя при разрыве волокна может стать значительным.

     Пониженная энергия поверхностного слоя приводит к всестороннему сжатию тела [30]. В твёрдых телах поверхностный слой находится в напряжённом состоянии. Особый интерес вызывает знание толщины поверхностного слоя, то есть глубины действия поверхностных сил. По работе [27] толщина поверхностного слоя твёрдого тела в результате взаимодействия частиц оценивается в 0,1-1,0 нм.

     Поверхностная энергия является индивидуальной характеристикой вещества и определяется в первую очередь его химическим составом. В работе [28] указывается, что на поверхностную энергию твёрдого тела оказывает влияние также предыстория поверхности, особенности её формования. В связи с неоднородностью материала поверхностная энергия может быть различной в разных точках тела.

     Для разрушения твёрдого тела необходимо затратить работу по удалению частиц на расстояния, при которых прекращается их взаимодействие. Это значит, что нужно преодолеть межатомные силы взаимодействия в поверхностном слое и внутренней части тела. Так как прочность поверхностного слоя твёрдого тела в нормальных условиях всегда больше прочности внутренней части, то увеличение относительной доли площади поверхностного слоя в поперечном сечении увеличивает прочность тела. Если среднее разрывное напряжение гипотетического бездефектного стеклянного волокна  σ, то для внутренней части и поверхностного слоя средние разрывные напряжения будут соответственно  σ₁  и  σ₂, причём,  σ₂  всегда больше  σ₁. Как указывалось выше, величина  σ₂ – σ₁  зависит от химического состава стекла, условий формования и предысторией поверхности.

     Возьмём стеклянные волокна одного химического состава различной толщины. Учитывая, что прочность поверхностного слоя значительно превышает прочность внутренней части, с уменьшением диаметра волокна возрастает и его прочность. Независимо от диаметра волокон до определённого предела толщина поверхностного слоя стёкол одного химического состава будет одинаковой. Обозначим толщину поверхностного слоя через  δ  и радиус внутренней части через  r. Площади поперечного сечения внутренней части  S₁  и поверхностного слоя  S₂  будут:

S₁ = π r²,   S₂ = π (2rδ + δ²).

Общее разрывное усилие волокна:

P = π r² σ₁ + π (2rδ + δ²) σ₂.             (1)

Разделив обе части равенства (1) на общую площадь волокна  π R²,  где  R = r + δ , после преобразований получим удельную разрывную прочность волокна:

σ = σ₁*r²/R² + σ₂ (1 – r²/R² ) = σ₂ – r²/R² *(σ₂ – σ₁ ).         (2)

Так как для волокон одного химического состава при идентичных условиях выработки  δ = const,  выразим радиус внутренней части волокна  r  через толщину поверхностного слоя  δ:

r = n δ.                                             (3)

Учитывая, что  R = r + δ,  подставляя (3) в (2), получим:

σ = σ₂ – n²/(n +1)²* (σ₂ – σ₁ ).           (4)

Это удельная прочность волокна в зависимости от  σ₁,  σ₂  и радиуса волокна  R, выраженного через число толщин поверхностного слоя  n. Формула (4) справедлива только до диаметра такого волокна, в котором в поперечном сечении площадь внутренней части волокна и площадь поверхностного слоя равны. В этом случае толщина поверхностного слоя волокна остаётся равной толщине поверхностного слоя в массивном стекле.

     Толщина поверхностного слоя зависит от химического состава стекла и условий формования. Поэтому для волокон одного диаметра, но различного химического состава  n  в (3) будет различным. Несмотря на это,  n  характеризует зависимость прочности от диаметра волокна. В свою очередь σ₁  и  σ₂  также являются индивидуальными характеристиками для некоторого состава стекла.

     В зависимости от величины  σ₁  и  σ₂  для различных стёкол по формуле (4) можно построить теоретическую номограмму, семейство кривых которой отражает удельную прочность стеклянных волокон от значения  n = r/δ – радиуса внутренней части волокна, выраженного в толщинах поверхностного слоя. По такой номограмме, кривые которой строятся при различных теоретических значениях  σ₁  и  σ₂ , можно определить величины  σ₁  и  σ₂  реального стеклянного волокна данного химического состава при сравнении экспериментальной кривой с кривыми номограммы.

     Кривые удельной прочности стеклянного волокна от величины радиуса в зависимости от химического состава стекла отличаются между собой. Это отличие определяется значениями  σ₁ , σ₂  и  δ. Такие разнообразные экспериментальные кривые зависимости прочности волокон от диаметра для разных химических составов приведены в работе [32]. На рис. 1 представлена экспериментальная кривая зависимости прочности на разрыв стеклянного волокна от его диаметра по [31].

 

 

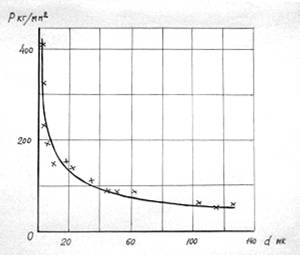
Рис. 1. Зависимость прочности на разрыв стеклянного волокна от его диаметра.

 

     Из формулы (4) следует, что поверхностный слой вносит свой вклад в повышение прочности только в тонких волокнах. Так, например, при  n = 50  член  n²/(n + 1)² = 0,96, то есть практически повышенная прочность поверхностного слоя не оказывает влияния на среднюю удельную прочность волокна. Теоретическая кривая, построенная по формуле (4) в зависимости от величины радиуса внутренней части волокна, выраженного через  n,  приведена на рис. 2. Эта кривая построена при значениях удельного разрывного напряжения внутренней части волокна  σ₁ = 500 МН/м²  и поверхностного слоя  σ₂ = 5000 МН/м² и представляет суммарную удельную прочность волокна  σ   для данного химического состава, которая является физической характеристикой материала. Как видно из рисунков, экспериментальная и теоретическая кривые идентичны по характеру. Такое сходство кривых зависимости прочности волокна от его диаметра подтверждает постулат о повышенной прочности поверхностного слоя конденсированных тел по сравнению с внутренним объёмом. Повышенная прочность поверхностного слоя соответствует его пониженной энергии.

 

 

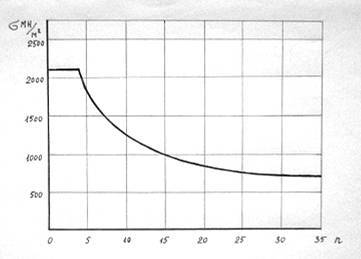
Рис. 2. Зависимость удельной прочности тонких волокон на разрыв от величины

их радиуса, выраженного в толщинах поверхностного слоя  n.

 

     Удельная прочность волокна при уменьшении диаметра будет возрастать до тех пор, пока поверхностный слой сохраняет свою толщину такой, какая она в массивном стекле. Дальнейшее уменьшение диаметра волокна изменяет геометрические размеры поверхностного слоя: начинается перераспределение площадей внутренней части и поверхностного слоя. С какого же диаметра волокна толщина поверхностного слоя начнёт уменьшаться? Поверхностный слой любого конденсированного тела находится в сжатом состоянии [30]. Для того, чтобы стабильно сохранялось равновесие между напряжениями сжатия поверхности и растяжения внутренней части, для цилиндрического тела в сечении площадь поверхностного слоя должна быть равна площади внутренней части.

     Из равенства площадей поверхностного слоя и внутренней части находим радиус внутренней части, выраженный в толщинах поверхностного слоя. Этот радиус будет равен 2,41, а радиус волокна 3,41 в толщинах поверхностного слоя. Если радиус волокна будет 3,41 толщин поверхностного слоя, в таком волокне поверхностный слой не отличается от массивных стёкол и реализует всю свою повышенную прочность. Из соотношения радиуса волокна в толщинах поверхностного слоя и радиуса внутренней части следует, что толщина поверхностного слоя, выраженная в толщинах поверхностного слоя массивного стекла в волокнах с радиусом менее 3,41 составляет 0,293 n, а радиус внутренней части 0,707 n, где  n – радиус волокна, выраженный в толщинах поверхностного слоя массивного стекла.

     Это соотношение остаётся справедливым для всех волокон с радиусом менее 3,41 n. Так как по формуле (2) отношение радиусов  r²/R²,  то есть  (0,707n)²/(0, 707n + 0,293n)² будет постоянным, то удельная разрывная прочность этих волокон также будет постоянной величиной. На графике рис. 2 удельная разрывная прочность таких волокон представляет прямую линию. Уменьшение диаметра этих волокон приводит просто к уменьшению их прочности в связи с уменьшением площади поперечного сечения.

     Найдём толщину поверхностного слоя волокна  δ, которая идентична поверхностному слою массивного тела. Подставляя в уравнение (1)  r =R – δ, решим его относительно  δ:

δ² – 2Rδ + (σ – σ₁ /σ₂ – σ₁ )*R² = 0.

Обозначив  (σ – σ₁ /σ₂ – σ₁ ) = a, найдём значение  δ. Так как  δ  всегда меньше  R, то:

δ = R [1 – √(1 – a)].                (5)

     Толщину поверхностного слоя экспериментального волокна можно найти, определив его сходство с теоретической кривой по номограмме, построенной по уравнению (4) при различных  σ₁  и  σ₂ . Из экспериментальных значений удельной прочности волокна  σ  и соответствующем ему радиуса волокна  R  рассчитывается величина  a. Заметим, что  a  является безразмерной величиной. Затем по формуле (5) определяется толщина поверхностного слоя волокна, соответствующего толщине поверхностного слоя массивного стекла данного химического состава. Для волокна, представленного на экспериментальной кривой рис. 1, получаем толщину поверхностного слоя около 1 мкм. Это значительно превосходит толщину поверхностного слоя по приближённым оценкам работ [17] в  5-10 нм  и [27] в  0,1-1,0 нм.

     Возможность дифференцированного определения по формуле (4) удельной прочности внутренней части и поверхностного слоя твёрдого тела при известной величине поверхностной энергии открывает перспективу для расчёта внутренней энергии твёрдых тел.

     Из формулы (4) вытекает, что высокая прочность тонких волокон заложена в повышенной удельной прочности поверхностного слоя. Повышенная прочность поверхностного слоя твёрдых тел определяется пониженной поверхностной энергией по сравнению с внутренними частями тела. Следовательно, ответственной за высокую прочность гипотетических бездефектных тонких стеклянных и других волокон (и тонких плёнок) является только поверхностная энергия. Прочность тонких волокон не может служить критерием для оценки прочности структуры массивного стекла, которая определяется удельной прочностью внутренней части.

     При переходе от гипотетических к реальным стеклянным волокнам (и другим волокнам и тонким плёнкам) на их прочность оказывают влияние различные дефекты. Однако, при определённом уровне дефектности прочность волокон (и тонких плёнок) определяется именно поверхностной энергией материала.

     Из представлений Гиббса [33] и других авторов [27-29] считающих, что поверхностный слой конденсированных тел имеет сгущение энергии, нельзя объяснить сверхвысокой прочности тонких волокон. Поэтому высокая прочность стеклянных волокон по сравнению с массивным стеклом стала проблемой физики твёрдого тела [34].

 

ВЫВОДЫ:

     1. Построена математическая модель, описывающая прочность тонких стеклянных волокон.

     2. Аналогия в ходе теоретической и экспериментальной кривых прочности стеклянных волокон подтверждает, что поверхностный слой стёкол прочнее внутренней части.

     3. В отличие от существующих гипотез высокой прочности тонких волокон в основу модели положено явление пониженной энергии поверхностного слоя.

     4. Показано, что глубина поверхностного слоя значительная. Это указывает, что поверхностные явления необходимо всегда рассматривать как трёхмерные.

     5. При уменьшении диаметра волокон удельная прочность растёт до определённого предела, когда радиус волокна станет равным 3,41 толщин поверхностного слоя массивного тела.

     6. С уменьшением диаметра волокна, когда его радиус меньше 3,41 толщины поверхностного слоя массивного тела, удельная разрывная нагрузка становится постоянной и прочность волокна уменьшается с уменьшением диаметра.

     7. При уменьшении диаметра волокна, когда уже достигнута максимальная прочность, происходит перераспределение площадей поверхностного слоя и внутренней части, чтобы обеспечить равновесие сжимающих и растягивающих напряжений.

     8. Высокая прочность волокон связана только с поверхностным слоем и не может быть использована для оценки прочности массивного стекла.

 

 

ЛИТЕРАТУРА

 

1. Т.Н.Кешишян, М.Б.Эпельбаум. Стекло и керамика, 12. № 7, 1958.

2. Ф.Ф.Витман, В.А.Берштейн, В.П.Пух. В кн.: Прочность стекла, 7. Мир, М., 1969.

3. A.A.Griffith. Phil. Trans. Roy. Soc., 163. ser. A, vol. 221, № 587, 1920.

4. А.П.Александров, С.Н.Журков. Явление хрупкого разрыва, 52. ГТТИ. М.-Л., 1933.

5. Т.А.Конторова. ЖТФ, 436. 15, 7, 1945.

6. Г.М.Бартенев. А.Н.Бовкуненко. ЖФХ, 508. 29, 3, 1955.

7. Т.Н.Кешишян, М.Б.Эпельбаум. Стекло и керамика, 9. № 8, 1959.

8. М.Б.Эпельбаум. Стекло и керамика, 10. № 1, 1963.

9. М.С.Асланова. В сб.: Стеклообразное состояние, 391. Изд. АН СССР. М.-Л., 1960.

10. М.С.Асланова. Современные воззрения на прочность стеклянного волокна, 32. М., 1965.

11. Г.М.Бартенев. В сб.: Стеклообразное состояние, 380. Изд. АН СССР, М.-Л., 1960.

12. Г.М.Бартенев. Сверхпрочные и высокопрочные неорганические стёкла, 240. Стройиздат, М., 1974.

13. B. Chatenet. Thase doct. ing. Le Centre Univ. du Haut Rhin. Et L’Univ. Lous Pasteur de Strasbourg, 77. 1971.

14. К.И.Блох. В сб.: Стеклообразное состояние, 423. Наука, М.-Л., 1965.

15. М.С.Асланова. Стекло и керамика, 1. № 4, 1967.

16. П.С. Калинин, Р.С.Шевелевич. Изв. АН СССР. Неорган. матер., 1891. 7, № 10, 1971.

17. Г.М.Бартенев, Л.К.Измайлова. В сб.: Стеклообразное состояние, 426. Наука, М.-Л., 1965.

18. Г.М. Бартенев. Строение и механические свойства неорганических стёкол, 216. Стройиздат, М., 1966.

19. Г.М.Бартенев, Р.Г.Черняков. Изв. АН СССР. Неорган. матер., 411. 4, № 3, 1968.

20. Г.М.Бартенев. Стекло и керамика, 4. № 8, 1967.

21. Г.Д.Андреевская. Высокопрочные ориентированные стеклопластики, 369. Наука, М., 1966.

22. Ф.К.Алейников, Р.Б.Паулавичюс, В.А.Парфенов, 7. Тр. АН Лит. ССР, сер. Б, № 1(40), 1965.

23. У.Б.Хиллинг. В кн.: Прочность стекла, 68. Мир, М., 1969.

24. Ф.М.Эрнсбергер. В кн.: Прочность стекла, 33. Мир, М., 1969.

25. Г.М.Бартенев. В кн.: Механические и тепловые свойства и строение неорганических стёкол, 54. ВНИИЭСМ, М., 1972.

26. А.П.Савицкий. В кн.: Смачиваемость и поверхностные свойства расплавов и твёрдых тел, 201. Наукова думка, Киев, 1972.

27. В.Д.Кузнецов. Поверхностная энергия твёрдых тел, 220. ГИТТЛ, М., 1954.

28. А.А.Берлин, В.Е.Басин. Основы адгезии полимеров, 391. Химия, М., 1974.

29. Н.Н.Круглицкий. Основы физико-химической механики, ч. 1, 263. Вища школа, Киев, 1975.

30. А.И.Болутенко. Научные гипотезы. Физика стекла, гип. 3, 1978.

31. Справочник по производству стекла, т.1, 1026. Под. Ред. И.И.Китайгородского и С.И.Сильвестровича, Стройиздат, М., 1963.

32. М.С.Асланова, С.З.Вольская. В сб.: Стеклообразное состояние, 428. Наука, М., 1965.

33. Дж.В.Гиббс. Термодинамические работы. ГИТТЛ, М.-Л., 1950.

34. В.П.Пух. Прочность и разрушение стекла, 23. Наука, Л., 1973.

 

12.12.1978

 

Публикация 1.01.2012