ТЕОРИЯ ПРОЧНОСТИ СТЕКЛА НА РАСТЯЖЕНИЕ
Прочность стекла
А.И.БОЛУТЕНКО
E-mail: bolutenko@mail.ru Физика стекла Главная
АННОТАЦИЯ
Разработана теория разрыва твёрдого абсолютно
упругого тела из теории строения стекла и механизма разрыва химических связей.
Дискретное распределение химических связей в стекле по их силе определяет
прочность стекла на растяжение. Прочность стекла характеризуется прочностью
наиболее сильных связей. Наличие в стекле связей с различной прочностью
предопределяет, что стекло – материал с низкой прочностью на растяжение.
Среди всех практических свойств твёрдых
тел наиболее важным является прочность. Механическая прочность кристаллических
твёрдых тел главным образом зависит от дислокаций [1] и структуры [2].
Неизученность структуры стекла и отсутствие теории стеклообразного состояния
приводит к значительным затруднениям интерпретации результатов при исследовании
механических свойств стекла.
Автор работы [3] считает, что стекло благодаря неупорядоченной структуре
должно отличаться высокой прочностью, так как источники образования микротрещин
в структуре стекла находятся в высокодисперсном состоянии. Так как аморфная
структура не позволяет развиваться дислокациям [4], приводящим к деформированию
и разрушению металлов, прочность стекла должна быть выше, чем у металлов.
В связи с невозможностью пластического
течения в стекле даже при отсутствии экспериментальных данных из теории
вытекает, что стекло должно обладать исключительной прочностью [5]. Изменилось
отношение к стеклу как к малопрочному материалу [6], даже ставится вопрос о
получении высокоэластичных стёкол [7]. По [4] стекло имеет высокую природную
прочность, однако, большое количество дефектов не позволяет получить эту
прочность.
Несмотря на предположения о высокой
прочности до сих пор по традиционной технологии не получено стёкол с
высокопрочной структурой. В проблеме прочности много внимания уделяется
определению теоретической прочности стекла. В связи с неопределённостью
структуры теоретическая прочность оценивалась косвенными методами.
Теоретическая прочность стекла по расчётам достигает 2500 кг/мм2
[8]. Несмотря на огромную теоретическую прочность практическая прочность стёкол
на растяжение мала и составляет 5-15 кг/мм2. Невоспроизводимость результатов при
определении механической прочности стёкол не случайна, а является отражением
условий его производства [9].
Прочность стекла определяется его
структурой, дефектами образца, а также в значительной степени зависит от
условий испытаний. Трудности в интерпретации результатов исследования
механической прочности стёкол связаны со сложностью явлений, происходящих при
разрушении, которые являются результатом взаимодействия целого ряда факторов
при нагружении образца. В этой связи важным становится вопрос истинной
прочности стёкол при разрушении, не зависящей от дефектов и внешних условий, а
определяемой структурой материала. Представления о процессе разрушения твёрдых
тел могут быть основаны только при рассмотрении атомного механизма реакции тела
на воздействие внешней силы. Трещины, неоднородности и многие другие дефекты
твёрдых тел должны рассматриваться как вторичные факторы, оказывающие
значительное, а порой решающее, влияние на прочность. Это действие дефектов на
прочность твёрдого тела маскирует природу собственной прочности тела,
определяемой его структурой.
Первая теория прочности стекла предложена
А.Гриффитсом [10]. Для объяснения процесса разрушения стёкол предполагалось,
что в стекле имеются микротрещины. При нагружении образцов в вершинах
микротрещин происходит перенапряжение и последующий разрыв связей. Наличие в
стёклах тончайших трещин, которые находятся во всём объёме образца, Гриффитс
объяснил несоответствие технической и теоретической прочности.
Главный упор в теории Гриффитса делается
на наличие в стекле микротрещин до начала разрушения. Однако, в работе [11]
предполагается, что наличие микротрещин в стекле до начала разрушения
необязательно, и они могут зарождаться самопроизвольно. По работе [12]
микротрещины не обязательно должны быть неотъемлемой особенностью структуры,
возникновение их может быть чисто случайным.
При электронно-микроскопическом изучении
оптических кварцевых стёкол дефектов в виде микротрещин различных размеров,
наличие которых предполагал Гриффитс, не обнаружено [13]. Трещины могут
возникать в процессе изготовления образца или во время его нагружения, однако,
вопрос о происхождении микротрещин до сих пор не решён ввиду отсутствия
надёжных методов их обнаружения [14].
Статистическая теория прочности исходит из
того, что в стекле имеются дефекты, которые распределены статистически [15,
16]. Прочность образца определяется наиболее опасным дефектом. Так же, как и по
теории Гриффитса, статистическая теория предполагает наличие в образцах
дефектов различной степени опасности.
В противоположность чисто механическим
представлениям о разрыве твёрдого тела в последнее десятилетие получила
развитие кинетическая концепция разрушения твёрдых тел [11]. Основы этой
концепции заложены в работах [17, 18], исходя из представлений о тепловом
движении атомов. Разрушение твёрдого тела определяется как тепловым движением
атомов, так и механическими напряжениями.
Несмотря на наличие ряда теорий прочности
для стёкол ещё не создана молекулярная теория разрыва и не найдена природа
элементарных нарушений, определяющих прочность. Рассмотрим прочность стекла на
основе представлений о его структуре. По модели строения [19] в стекле
существует дискретный спектр химических связей по их силе (Рис. 1).
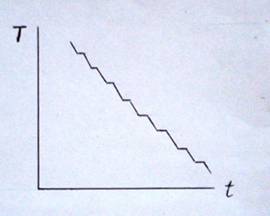
Рис.1
Фазовые переходы стеклообразных расплавов в твёрдое состояние
при охлаждении и структурообразование
стёкол [19].
Каждая структурная группа связей
на графике зависимости температуры от времени имеет свою линию ликвидуса. Чем
выше температура затвердевания структурной группы, тем большую энергию
необходимо затратить для её расплавления. Поэтому высокотемпературные
структурные группы твёрдого тела имеют более высокую прочность. Таким образом,
в твёрдом теле имеется целый ряд уровней прочности в структуре от максимальных
высокотемпературных до минимальных низкотемпературных. В зависимости от
химического состава стекла в нём может варьироваться периодичность дискретных
связей по их силе, причём, количество одинаковых по силе связей может быть
различным.
В зависимости от строения атомов в
структуре стекла и взаимодействия с соседними атомами связь каждой пары атомов
характеризуется жёсткостью и допустимым относительным удлинением, которые
определяют силу связи [20]. Пары атомов, имеющие одинаковые относительные
удлинения при растяжении, образуют уровни по силе связи.
Возьмём элементарный изотропный микрообъём
стекла без остаточных напряжений и приложим к нему малую растягивающую силу.
Рассмотрим поведение атомов стекла в будущей плоскости разрыва. Каждая пара
атомов находится под напряжением σ
= P/n, где P –
действующая сила, n – количество атомов в поперечном сечении микрообъёма.
По мере увеличения растягивающей силы P напряжения на
химические связи растут. Если в стекле данного химического состава имеется m уровней по силе связи, то n = n1 +n2 +… +n m, где n1 +n2 +… +n m – количество связей в каждом уровне. Для каждого уровня
допустимые разрывные напряжения соответственно будут: σ1, σ2,
…σm. Стекло является абсолютно
упругим твёрдым телом, пластические деформации в нём невозможны в связи с
различием характера соседних химических связей [19, 21].
При статическом увеличении действующей на
микрообъём силы, с достижением величины растягивающих напряжений в поперечном
сечении образца во всех связях до σ1
, химические связи n1 ,
имеющие допустимые разрывные напряжения
σ1 , разорвутся.
По своей конституции атомы с разорванными связями находятся в диссоциированном
состоянии и представляют собой вязкую фазу в упругом твёрдом теле [22].Тело
становится упруго-вязким, в нём ответственной за прочность является упругая
твёрдая фаза.
С разрывом самых слабых связей n1 действующая в
данный момент на микрообъём стекла сила P мгновенно
перераспределится на оставшиеся связи n – n1 и на каждую из
них в квазистатическом процессе будет действовать сила P/(n – n1 ). Однако, в момент разрыва самых слабых связей n1 при мгновенном
приложении нагрузки, которую несли разорвавшиеся связи, к остальным связям,
появляется динамическая составляющая силы, приходящейся на разрыв связей n1 . Общая добавленная сила на оставшиеся связи с учётом
динамической составляющей будет равна удвоенной силе, приходящейся на разрыв
самых слабых связей [20].
Когда разрываются самые слабые связи,
система немедленно реагирует на этот факт. Разрыв связей в системе, находящейся
в равновесии, ведёт к изменению местоположения остальных атомов – система деформируется
для сохранения устойчивости. Дальнейшее повышение растягивающей нагрузки до
напряжений σ2 на связь приводит к разрыву следующего уровня
связей n2 и так далее, пока не произойдет полный разрыв
тела. Таким образом, по мере нарастания нагрузки происходит последовательный
разрыв связей, имеющих допустимые разрывные напряжения меньше создаваемых
действующей силой и инерционной составляющей разорвавшихся связей. Нагрузка
мгновенно перераспределяется на оставшиеся связи.
Рассмотрим, что представляет собой
элементарный акт разрыва химической связи. При приложении растягивающей
нагрузки происходит диссоциация слабых связей с малым допустимым удлинением.
Нагрузку после разрыва слабых связей несут сильные связи с максимально
допустимыми относительными удлинениями. Разрыв различных по силе химических
связей хорошо демонстрирует механическая модель, когда последовательно
разрываются связи одной группы за другой. Надо взять n нитей разной длины и связать их
противоположные концы в узлы, а затем растягивать их. Положим, что каждая нить
разрывается при нагрузке P, то такая система разрушится не силой Pn, а
силой P.
Если образец из стекла не доводить до
разрушения, то после снятия нагрузки диссоциированные химические связи
ассоциируют. Локальные микроразрывы в результате диссоциации слабых связей
образуются только в нагруженном растягивающей силой стекле.
До и после нагружения микроразрывов в стекле нет. Становится
понятным, почему не были экспериментально обнаружены трещины Гриффитса в
ненапряжённых образцах стекла. Для разрушения образца локальные микроразрывы
слабых связей не имеют существенного значения. Прочность стекла определяется не
суммой прочностей всех химических связей в плоскости разрыва и не структурными
микротрещинами, а прочностью наиболее сильных связей.
Устойчивость образца при воздействии
растягивающей силы P сохраняется,
когда P‹ σί (n –nί), то есть в теле имеется некий уровень удельных
напряжений на связь σί
, произведение которого на количество неразрушенных связей превышает
действующую силу P . Если P› σί (n –nί), происходит разрушение следующего уровня связей в
теле. Как указывалось выше, динамическая составляющая силы P при разрыве атомных связей ί-го уровня вносит дополнительное
увеличение действующих растягивающих напряжений на остальные связи. Поэтому по
своей конституции стекло является малопрочным материалом, несмотря на
невозможность развития в нём дислокаций.
Процесс разрушения стекла представляет
собой последовательный разрыв структурных групп химических связей по их силе.
После разрыва самых слабых связей нагрузка перераспределяется на оставшиеся
связи. Хотя визуально образец сохраняет живое сечение, при уровне напряжений,
способных разрушить самые слабые связи, наступает лавинообразный перенос нагрузки
с динамической составляющей силы, разорвавшей этот уровень связей, на другие
связи. После последовательного разрыва ряда уровней связей по их силе при
наступлении перегрузки связей, оставшихся ещё целыми в некоторый момент
времени, происходит мгновенное взрывоподобное их разрушение. Механизм
разрушения химических связей стекла предопределяет его низкую прочность на
растяжение.
ВЫВОДЫ
1. Разработана теория разрыва твёрдого
абсолютно упругого тела непосредственно из механизма разрыва химических связей.
2. Дискретное распределение химических
связей в стекле по их силе определяет его прочность на растяжение.
3. Механизм разрушения стекла при
растяжении представляет последовательный разрыв химических связей по их силе
при лавинообразном нарастании напряжений на ещё не разорванные связи.
4. Прочность стекла определяется не суммой
прочностей всех химических связей в сечении разрыва и не структурными
микротрещинами, а прочностью наиболее сильных связей.
5. В ненагруженном стеклянном образце
отсутствуют структурные микротрещины. Они возникают при напряжениях растяжения
в результате диссоциации атомов слабых связей. Снятие напряжений приводит к
ассоциации слабых связей.
6. Наличие в стекле связей с различной
прочностью предопределяет, что стекло – материал с низкой прочностью на
растяжение.
7. Низкая прочность массивного стекла на
растяжение, более чем на два порядка ниже теоретической, свидетельствует, что в
основу построения теории о высокой прочности стекла положены ошибочные
представления о стекле как аморфном теле.
8. Теория строения стекла как
поликристаллического абсолютно упругого твёрдого тела с неопределённым составом
структурных групп и различной их механической прочности успешно объясняет
низкую прочность массивного стекла на растяжение.
ЛИТЕРАТУРА
1. Ч.Уэрт, Р.Томсон. Физика
твёрдого тела, 142. Мир, М., 1969.
2. Г.М.Бартенев. Сверхпрочные
и высокопрочные неорганические стёкла, 240. Стройиздат, М., 1974.
3. И.А.Богуславский. Высокопрочные
закалённые стёкла, 151. Стройиздат, М., 1969.
4. В.П.Пух. Прочность и
разрушение стекла, 155. Наука, Л., 1973.
5. У.Б.Хиллинг. В кн.:
Прочность стекла, 68. Мир, М., 1969.
6. Ф.Ф.Витман, А.А.Берштейн,
В.П.Пух. В сб.: Прочность стекла, 7. Мир, М., 1969.
7. А.Н.Лазарев. В кн.:
Структурные превращения в стёклах при повышенных температурах, 233. Наука,
М.-Л., 1965.
8. И.Нараи-Сабо. В сб.:
Стеклообразное состояние, 74. Наука, М.-Л., 1965.
9. С.М.Бреховских,
В.М.Кулаков. В кн.: Механические и тепловые свойства и строение неорганических
стёкол, 36. ВНИИЭСМ, М., 1972.
10. A.A.Griffith. Phil. Trans. Roy. Soc., 163. ser. A, vol. 221, № 587,
1920.
11. С.Н.Журков. Неорг.
материалы, 3, № 10, 1767, 1967.
12. Ф.М.Эрнсбергер. В кн.:
Прочность стекла, 33. Мир, М., 1969.
13. Ф.К.Алейников. ДАН СССР,
156, 154, 1964.
14. П.Я.Бокин. Механические
свойства силикатных стёкол, 180. Наука, Л., 1970.
15. Т.А.Конторова,
Я.И.Френкель. ЖТФ, 11, 173, 1941.
16. Б.Б.Чечулин. ЖТФ, 24,
292, 1954.
17. С.Н.Журков,
Б.Н.Нарзуллаев. ЖТФ, 23, 1677, 1953.
18. С.Н.Журков. Вестн. АН
СССР, 11, 78, 1957.
19. А.И.Болутенко. Научные гипотезы. Физика стекла, гип. 1, 1977.
20. А.И.Болутенко. Научные гипотезы. Физика стекла, ст. 14, 1979.
21. А.И.Болутенко. Научные гипотезы. Физика стекла, ст.12, 1978.
22. А.И.Болутенко. Научные гипотезы. Физика стекла, гип. 2, 1978.
12.02.1979
Публикация 14.01.2012